무무키의 개발일지
벡터 및 미적분 공부 (1) 본문
오늘 공부한 점에 대해서 정리하듯이 적어보려고한다.
기호나 그림을 그려서 넣어야할지 만들어주는 사이트가 있는지 잘 몰라서 일단 공부한 내용으로 올립니다.
틀린 내용이 있다면 댓글로 알려주세요...강의를 보면서 노트필기를 하긴 하지만 틀린게 있을 수 도 있습니다!
데이터 여러개를 한줄에 담아낼 수 있게 만든 것: 벡터
벡터를 시작점과 끝점으로 연결하는 화살표로 표시 할 수 있음
하지만 시작점이 다르면 같은 벡터라도 끝점이 다를 수 있다.
글씨가 좋진 않지만 벡터 기호와 행렬 형태를 표현할 방법이 없어서 사진을 넣었다

벡터의 덧셈
(a,b,c) + (A,B,C) = (a+A,b+B,c+C)
어떤 벡터의 시작을 먼저해도 끝점은 같다(Parallelogram rule:평행사변형법)
a다음 b를 하는 것과 b 다음 a를 하는 것의 결과는 같다

스칼라 곱셈(스칼라배)
여기서 스칼라는 상수의 다른 이름
v = (a,b,c)일때 xv = (xa,xb,xc)
스칼라 곱셈은 벡터를 스칼라 배 만큼 길이를 늘리는 것이다.
스칼라가 -1이라면 방향을 바꾸는 것.
벡터의 크기(길이) (vector magnitude)
||a|| 나 |a| 로 정의한다. 벡터 (a,b)의 길이는 √(a^2+b^2) (피타고라스 정리)
<스칼라 곱(Dot Product)(내적)>
유클리드 공간의 두 벡터로부터 실수 스칼라를 얻는 연산
⃗ a· ⃗ b = || ⃗ a|| || ⃗ b|| cos(θ) (0 <= θ <= π) ( cos(θ)는 a와 b사이의 각도 )
- cos(θ)는 1 이기에 각도가 0, 같은 방향일수록 스칼라 곱이 더 크다.
- θ = π /2 일때 두 벡터는 직교하고 cos(π/2) = 0이므로 스칼라곱은 0
- 스칼라 곱은 두 벡터가 반대 방향이라면 음수가 될 수 있다 (π/2 < θ < 3π/2)
- 결과는 스칼라 이다. 그러므로 ⃗ a· ⃗ b· ⃗ c 의 결과는 벡터이다
- 스칼라곱은 어떤 길이에도 적용된다(차원)
⃗ a = (a1,a2), ⃗ b = (b1,b2) 일 때 ⃗ a· ⃗ b = (a1*b1+a2*b2)
위의 공식을 이해하려면 코사인 법칙이 사용된다고 했지만 코사인 법칙을 뭔지 몰랐기에
https://mathbang.net/537#gsc.tab=0 제 1 코사인 법칙 증명
https://mathbang.net/538#gsc.tab=0 제 2 코사인 법칙 증명
https://youtu.be/aXosYpzK90k 코사인 법칙 영상을 통해 다시 공부했다

유튜브 영상에서 둔각 삼각형에서의 코사인 법칙 증명을 보던 중
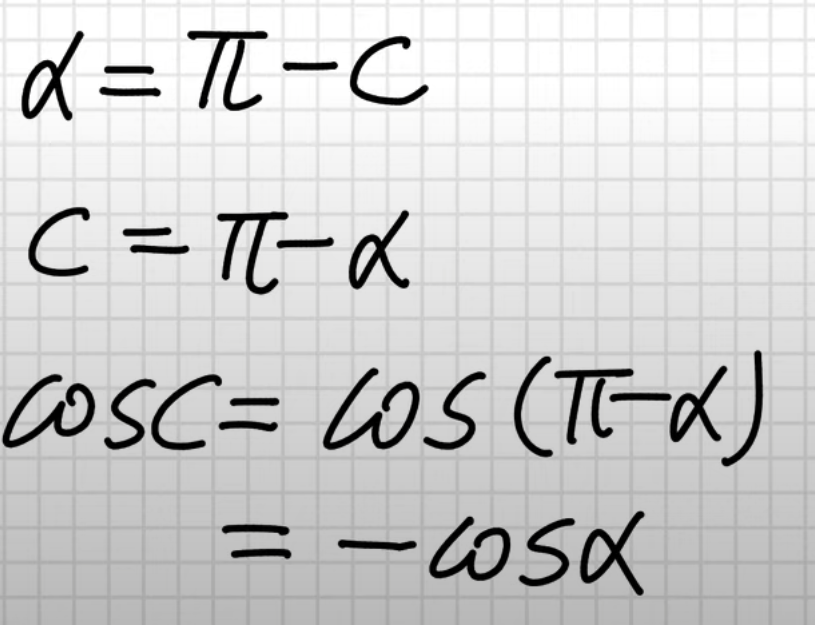
왜 코사인이 - 값을 가지게 되는지에 대해서 모르겠어서 한번 더 파고들어갔다.
원래였으면 필요한 정보만 알고 넘어갔어야 했지만 모두 기초에 해당하는 부분이라서 공부할때 탄탄히 알고싶었다.
https://mathbang.net/506#gsc.tab=0 에서 삼각함수의 각의 변환과

추가적으로 우함수 기함수 부분을 찾아보았다.
이제 공식의 증명을 이해할 준비가 모두 끝났다.
세변의 길이를 안다면 cos(θ)를 구할 수 있다는 것 / | ⃗ a|와 | ⃗ b|는 √(a1^2+a^2), √(b1^2+b^2) 인 것을 활용해
하나하나 증명을 풀어나가니 결국 내가 처음에 봤던 공식이 된 것이 너무나 신기하고 기뻤다
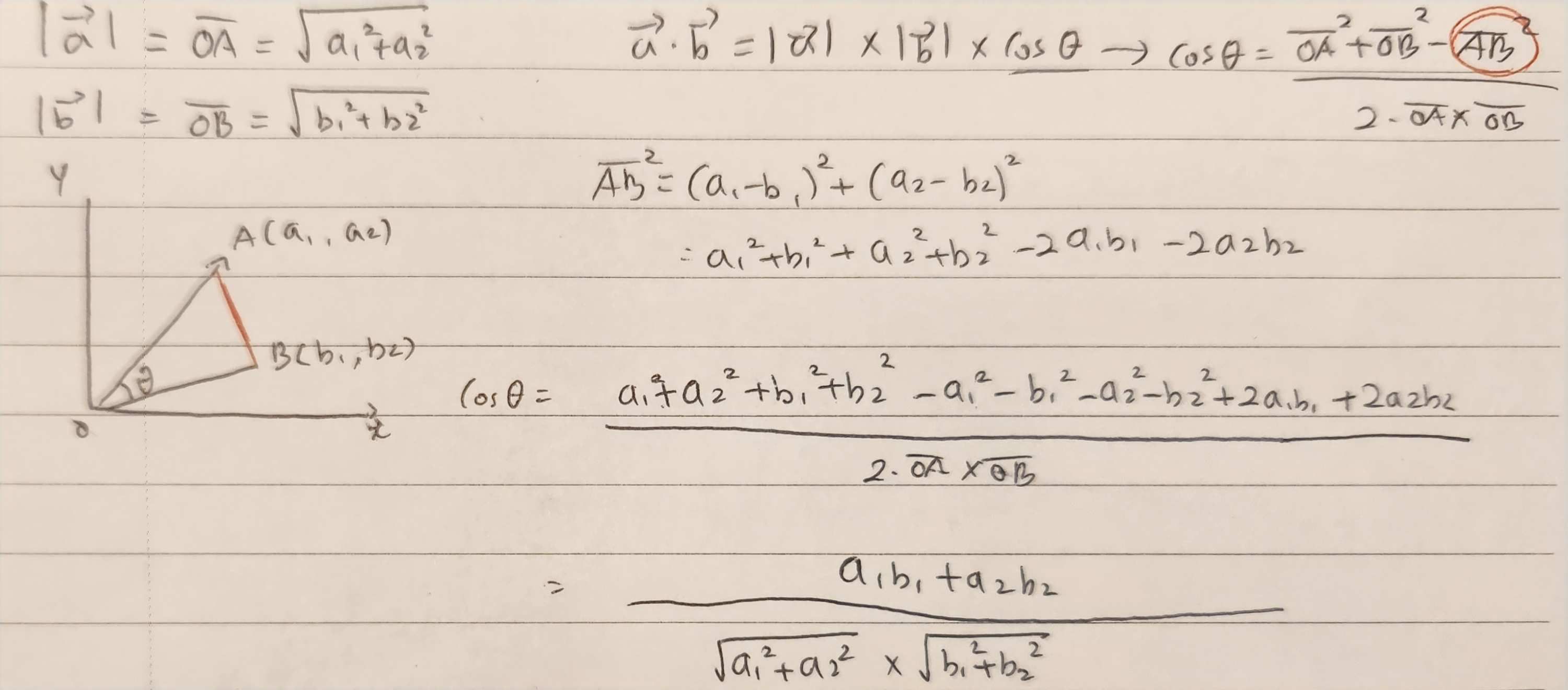

너무 깊게 파면서 공부하는게 아닌가 하는 생각이 든다.
코사인 법칙이나 우함수 기함수 등의 기초 수학을 계속 찾아가면서 공부해서 그런지 오래 걸리는 것 같다.
칸 아카데미 강의들보다는 계속 공부하던 인공지능을 위한 수학 책의 완벽 이해에 좀 더 시간을 들일 것 같다.
하지만 선형대수나 확률과 통계는 유튜브 영상이 자세하게 설명되어있어서 열심히 들어보고 있다.
노트에 정리가 끝나면 글로도 한번 올려보겠다.
